Accountability in the publishing process
Introduction
Yesterday the Retraction Watch blog published an article titled "Why publishing negative findings is hard". The article describes my attempts to set the record straight related to two controversial claims about the purported effects of the full moon.
The first part of the Retraction Watch article relates to the extraordinary claim that a certain plant pollinates during the full moon (Rydin and Bolinder, 2015). This claim received wide media coverage hailing the "discovery" of a "werewolf plant", with far-reaching implications for plant evolution. Unfortunately, this claim is based on only 3 data points. I wrote a paper that explains why the pollination study is both incorrect and incomplete, and why its conclusions are almost certainly wrong.
The second part of the Retraction Watch article relates to the extraordinary claim that the number of hospital admissions increases during the full moon. I wrote a paper that explains why the authors' data collection, analysis, interpretation, and conclusion are fatally flawed. I discuss this claim in a separate web article.
Retraction Watch is a specialty blog that tracks scientific retractions. While the rate of retractions of scientific papers remains quite low (fewer than 1 in 5000 publications, according to fivethirtyeight.com), this blog also includes stories about minor errors, conflicts of interest, and the difficulty of publishing negative results. This latest article recounts the considerable effort it took to publish my papers in the peer-reviewed scientific literature (roughly 5 times the amount of effort that it takes for a typical paper).
The Retraction Watch article is written in a fairly neutral tone. The article could have discussed the strength of the arguments for or against the controversial claims at issue, but it does not. The authors interviewed many of the actors and the article incorporates relevant quotes. The Retraction Watch article centers on the difficulty of publishing negative findings, not on the substance of the arguments. A negative finding often refers to a "null result", an experimental or observational outcome that does not show the anticipated effect.
A disappointing theme that pervades the quotes is that these authors, reviewers, and editors try hard to justify their actions at the expense of personal accountability. Before I discuss this issue, I will describe what my paper shows.
What my paper shows
In the first paragraph of my paper, I describe why Rydin and
Bolinder erred in using the correlation coefficient in their attempt
to establish a link between full moon and pollination.
They reported 3 pairs of points (red circles) representing days of
the pollination peak (with an uncertainty of about one day) and days
of the full moon in July (Figure 1).
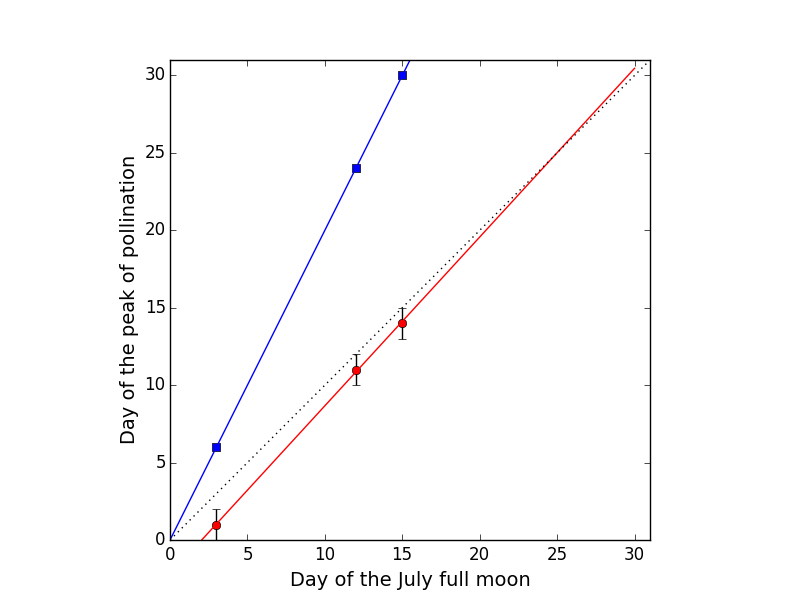 If the
coincidence between these events were perfect, the red points would
fall on the dotted line. The authors drew a line through their data
(red line), computed a quantity known as the correlation
coefficient, and found a value near 1. Unfortunately, the fact that
the correlation coefficient is near 1 is meaningless. To illustrate
why that is, I drew a set of hypothetical pollination dates (blue
squares) and the corresponding line (blue line). These data yield
the best possible correlation coefficient (equal to exactly 1), but
there is obviously no connection between the dates of pollination
and the full moon. So the correlation coefficient is an incorrect
metric to use in this problem. In any case, as we'll see below,
correlation does not imply causation.
If the
coincidence between these events were perfect, the red points would
fall on the dotted line. The authors drew a line through their data
(red line), computed a quantity known as the correlation
coefficient, and found a value near 1. Unfortunately, the fact that
the correlation coefficient is near 1 is meaningless. To illustrate
why that is, I drew a set of hypothetical pollination dates (blue
squares) and the corresponding line (blue line). These data yield
the best possible correlation coefficient (equal to exactly 1), but
there is obviously no connection between the dates of pollination
and the full moon. So the correlation coefficient is an incorrect
metric to use in this problem. In any case, as we'll see below,
correlation does not imply causation.
The second part of my paper describes the correct way of
quantifying the coincidence between events and the full moon. A good
way to think about this problem is to imagine that you are playing
what I call the lunar roulette (Figure 2).
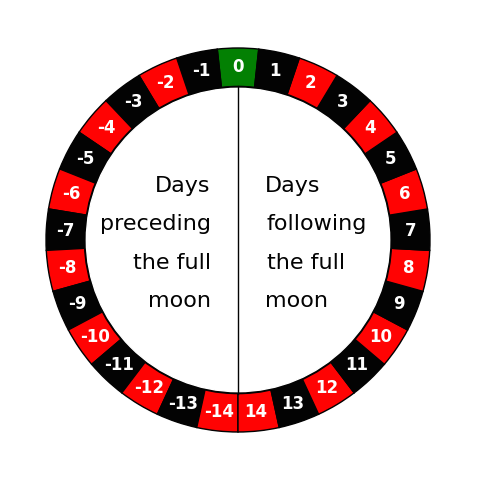 The event that
you care about (e.g., pollination peak) will either fall exactly on
the full moon (green pocket), or a number of days before or after the
full moon (red and black pockets). If you play repeatedly, and if you
consistently hit the green pocket or a small number, then you might be
entitled to ask whether there is a connection between the full moon
and the event that you are interested in.
The event that
you care about (e.g., pollination peak) will either fall exactly on
the full moon (green pocket), or a number of days before or after the
full moon (red and black pockets). If you play repeatedly, and if you
consistently hit the green pocket or a small number, then you might be
entitled to ask whether there is a connection between the full moon
and the event that you are interested in.
Rydin and Bolinder played the lunar roulette three times, and they obtained the sequence (-2, -1, -1). They believed that this sequence of small numbers indicated a connection between the full moon and plant pollination. Does it? My paper shows that this outcome is not particularly remarkable. There are 24389 possible outcomes when one plays the lunar roulette three times. Among those outcomes, 129 exhibit an equal or better coincidence with the full moon than what Rydin and Bolinder found. For instance, the sequences (0, 0, 0), (0, 0, 1), and (0, 0, -1) all exhibit a much better agreement with the full moon. The ratio of the two numbers, 129/24389, gives the probability that one will observe a coincidence with the full moon that is equal to or better than what Rydin and Bolinder observed. That probability is about 0.5%.
If you played the lunar roulette only 3 times and obtained a sequence of numbers as small as (-2, -1, -1), you might think that the outcome was unusual. Indeed, the probability of obtaining this sequence or a sequence that is even closer to (0, 0, 0) is only 0.5%. Rydin and Bolinder reasoned that there was something unusual to that sequence, but this reasoning is unsound. Botanists have not played the lunar roulette three times. They have played it hundreds of thousands of times. For centuries, they have meticulously recorded the dates of certain plant development phases (first leaf, first flower, pollination peak, etc) for hundreds of species. Statistically, we expect 0.5% of these hundreds of thousands of outcomes to show a close coincidence with the full moon, even if the moon has absolutely no effect on plants! In other words, we expect to find many examples of exquisite alignment with the full moon in the plant record.
My paper provides six examples of superb alignments with the full moon that have not been previously reported. For instance, the meadow foxtail in Reichenbach, Germany, flowered precisely on the day of the full moon in 1978, 1980, and 1981, a sequence that has a probability of occurrence of only 0.004%. This alignment is much better than that observed by Rydin and Bolinder, but it has nothing to do with the moon. We know that the flowering of this plant is unrelated to the moon because it is not synchronized with the full moon in subsequent years. In my paper, I predict that we will reach the same conclusion in the case of pollination that Rydin and Bolinder attribute to the full moon. We just need additional data.
In the last part of my paper, I show that one of the mechanisms invoked by Rydin and Bolinder to explain their data cannot possibly influence pollination. They postulated that lunar tides could affect the timing of pollination. There are two problems with this idea. First, lunar tides are quite weak compared to tides from ordinary objects on earth. A car parked 10 meters away has a tidal effect that is 1000 times stronger than the lunar tide. A botanist making an observation 1 meter away has a tidal effect that is 50000 times stronger than the lunar tide. Second, the strength of lunar tides is about the same at new moon and at full moon, but Rydin and Bolinder reported pollination only near full moon. For these two reasons, the proposed explanation is not plausible.
The reaction from the lead author
Rydin wrote that my paper does not contribute anything to science, does not provide new data, and does not report errors in her calculations. I disagree with all three assertions.
Rydin justified her publication with the following statement: "it is important to have the courage to present also quite bold hypotheses in order for science to progress." When a bold hypothesis is supported by sufficient data, and when all other obvious hypotheses have been ruled out, it is indeed appropriate to publish. In the pollination case, however, neither of these conditions were true. This publication resulted in an impediment to science, because it sent others on a wild goose chase for improbable lunar effects, because other scientists spent time performing the elementary tests that were not conducted before publication, and because the unsound claim polluted the scientific literature (e.g., this review article reports the pollination claim as a fact).
Rydin also wrote that "the risk of Type I errors is known to every scientist". A Type I error occurs when someone claims to have detected an effect that is not present. My paper argues that the rough coincidence that she observed on only 3 occasions is a Type I error. Had she allowed for that possibility in her paper, my analysis would have been unnecessary. Most careful scientists go out of their way to point out the possible limitations of their work, but the pollination paper included no cautionary statement.
Biology Letters
The editors at Biology Letters chose to publish an extraordinary claim based on only 3 data points, with absolutely no cautionary statement about the possibility of a spurious correlation. They also chose to reject my paper twice, even though it offered a more reasonable explanation of the same data.
The stated reasons for declining my paper were bizarre. The reviewers and editors did not discuss the merits of my paper, but rather focused on justifying why they felt that they had been right in publishing Rydin's paper in the first place. These considerations are irrelevant when evaluating my paper. I was not asking that Rydin's paper be retracted. I was merely proposing a different analysis and interpretation of her data. By refusing to publish my analysis, the editors prevented the kind of scientific conversation that enables progress in science.
The explanation that the editors gave to Retraction Watch is consistent with my recollection: "However, the reviewers of the comment were happy that the hypothesis itself remained valid, as were we, and this was the basis of our decision." In essence, the editors wrote that their reason for not publishing hypothesis #2 is that hypothesis #1 has not yet been disproved. But how does a hypothesis become disproved? By refusing to publish hypothesis #2, the editors perpetuated the very conditions that permit hypothesis #1 to "remain valid".
Science does not operate in the way that Biology Letters operate. Observations are made and hypotheses are proposed. The best answer is found by comparing and testing all the hypotheses that have merit. The reluctance of editors to publish corrections or alternate hypotheses is a considerable impediment to progress in science.
It is not the first time that Biology Letters makes editorial decisions that are not aligned with scientific principles. Retraction Watch will continue to monitor Biology Letters' editorial record.
The news media
After publishing my paper, I made a concerted effort to reach out to all the news outlets and bloggers who had reported on the initial "discovery" of a lunar influence on pollination. I contacted about a dozen writers via email or twitter, suggesting that they consider adding a cautionary note to their reports or describing the newly published interpretation. Only one writer changed her initial text describing an "undeniable correlation" to a more nuanced statement.
News media widely publicized the premature claim of a lunar influence on plants, but the overwhelming majority of reporters took no action to set the record straight when new evidence came to light. The reluctance of news media outlets to publish corrections to unsubstantiated or incorrect news stories contributes to a misinformed public.
Conclusions
It is unfortunate that some authors and editors are more interested in reacting defensively and in justifying their actions than admitting error and publishing corrections. News media outlets tend to ignore the need for corrections altogether. These attitudes need to change in order to enable scientific progress and accurate communication of scientific results to the public.